Zip-NeRF阅读

原文 Link: [https://zhuanlan.zhihu.com/p/645402002]

关于原文详细内容，我不会过多重复，可以去看原文以及下面的文章，总结的相当不错，不过在论文5月在arxiv上更新过一次内容。更新的部分我会进行一些补充，不过我也不是逐行对比，只会提到重要部分。

Zip-NeRF要点总结：

氵景页：Zip-NeRF 个人笔记

以及参考github上复旦老哥的复现：

SuLvXiangXin/zipnerf-pytorch: Unofficial implementation of ZipNeRF (github.com)

首先是上面这个图。回顾文中使用的六点采样。我会在下面详细说说这个采样，十分诡异。在这个图里，可以看出圆锥的截面圆是垂直于射线的，但在Mip-NeRF中截面圆与image plane平行，这一改动在文章里没有具体展开。上面那哥们在复现的时候还被一个老哥戳了这个地方修改了。我猜想是他们发现这样效果更好，毕竟原本用的就是自己的代码。

然后就是这个公式了。因为我一开始也是看的第一版文章，看到这个公式的时候居然忘记看他补充的解释了。。于是我暴力地计算猜想这个式子的意思。。现在看来实在是我浅薄了，但毕竟算都算了，整理一下思路。

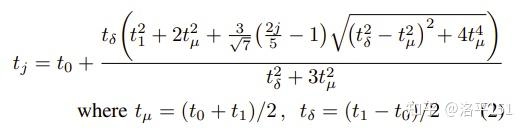
这个公式给出的是在一个区间里，采集的六个点在轴上的距离。结论是，这是在这个区间中，均匀地采样六个点，使得轴上的六个点均值方差等于这个圆台的高斯近似参数。

不得不说，这个式子看着很吓人，既没有优雅的中心对称性，也没有容易理解的化简形式，甚至还有 $\frac{3}{\sqrt{7}}$ 这种东西。

### 推导前置知识（推导过Mip-NeRF公式可跳过这段）：
关于$\dot r$。在Mip-NeRF中，这个参数出现在公式 $\left(\frac{\mathbf{d}^{\mathrm{T}}(\mathbf{x}-\mathbf{o})}{\|\mathbf{d}\|_2\|\mathbf{x}-\mathbf{o}\|_2}>\frac{1}{\sqrt{1+\left(\dot{r} /\|\mathbf{d}\|_2\right)^2}}\right)$ 中，文章将其设为 $\frac{2}{\sqrt{12}}$ 。这个公式很好理解，左边是向量夹角 $\cos \theta$ 的定义，右边也是一个角度，因为令 $\frac{\dot{r}} {\|\mathbf{d}\|_2}=\tan\theta_0$ ，右边就是 $\cos{\theta_0}$ 。这样看来，这个参数表征的是圆锥的顶角大小，实际意义是控制图像平面上的截面圆相对于像素边长的大小（原文：We set $\dot r$ to the width of the pixel in world coordinates scaled by $\frac{2}{\sqrt{12}}$）。至于数值设定，可以发现，令 $\|\mathbf d\|_2=1$ ，则恰好对应30°。我怀疑当初就是这么设定的。

接下来是Mip-NeRF中的采样点（高斯近似）计算，Mip-NeRF的补充材料第一部分推导写的很清楚。核心思想是使用一个高斯分布来近似一段截取的圆锥，那么高斯分布的参数就是这一段圆锥上所有点位置的期望和方差。方差计算就是按照定义得到的（ $\text{Var}(X) = \text{E}[X^2] - \text{E}[X]^2$ ）。计算结果是

$\begin{gathered} \mu_t=t_\mu+\frac{2 t_\mu t_\delta^2}{3 t_\mu^2+t_\delta^2}, \quad \sigma_t^2=\frac{t_\delta^2}{3}-\frac{4 t_\delta^4\left(12 t_\mu^2-t_\delta^2\right)}{15\left(3 t_\mu^2+t_\delta^2\right)^2} \\ \sigma_r^2=\dot{r}^2\left(\frac{t_\mu^2}{4}+\frac{5 t_\delta^2}{12}-\frac{4 t_\delta^4}{15\left(3 t_\mu^2+t_\delta^2\right)}\right) \end{gathered}$

结合起来看，发现和上面给出的 $t_j$ 有点像，但也只是有那么一点像。

## 公式推导及思路
我会想不明白 $t_j$ 的式子，一方面是因为我是初学且没看仔细，另一方面是这个式子给的形式十分变态，推测可能是符号计算用电脑算的。在给了 $t_\mu, t_\delta$ 的前提下，分子上还出现 $t_1$， 实在有点打错的嫌疑，也是这让我决心算到底。

首先考虑是不是等分体积，即等分位置期望，但随即意识到给出的坐标点是均匀的（然而愚昧的我过了好久才意识到。忌熬夜推公式）。如此一来，既然这六个点是用来近似这个高斯的，那么会不会是这六个点期望和方差是这个高斯分布，然后推出来的。这样的话，又有是轴上点方差还是投影点方差的问题，因为实际采的是圆锥边界上的点。

下面计算，如果是轴上点均值方差等于高斯参数的情况。东西太多，进入手算环节。

所以其实思路很简单，然后公式也没有给错。回到上面的猜想，Zip-NeRF没有使用在圆锥边界上的点计算方差近似高斯，很是奇怪，怀疑这一点是不是不太严谨。